Il sistema computazionale definitivo per risolvere i problemi tecnologici più all’avanguardia.
Per tre decenni, Mathematica ha definito lo stato dell’arte del calcolo tecnico e divenendo l’ambiente calcolo scelto da milioni di innovatori, tecnici, insegnanti e ricercatori in tutto il mondo.
Da sempre ammirato sia per la sua prodezza tecnica che per la sua elegante facilità d’uso, Mathematica fornisce un singolo sistema integrato, in continua espansione, che copre l’ampiezza e la profondità del calcolo tecnico – ed è perfettamente disponibile nel cloud attraverso qualsiasi browser web, così come nativamente su tutti i moderni sistemi desktop.
Adalta è Rivenditore Unico per l’Italia di Wolfram Mathematica. Richiesta quotazione…
Manutenzione
Introduzione a Mathematica
Grazie all’enorme varietà e potenza delle sue funzionalità native, Mathematica viene utilizzato in molteplici aree applicative e per diversi scopi: dall’insegnamento di semplici concetti in classe fino alla ricerca avanzata su grid di calcolo HPC. Con milioni di utenti nelle comunità educative e tecniche nel mondo Mathematica è la soluzione software definitiva.
Didattica con Mathematica
Mathematica offre un’esperienza interattiva in classe che aiuta gli studenti a esplorare e padroneggiare i concetti, inoltre fornisce ai docenti gli strumenti necessari per creare con semplicità materiale di supporto ai corsi, verifiche e presentazioni.
Gli studenti possono manipolare e ricalcolare i risultati in tempo reale, presentarli a un gruppo o rispedirli all’insegnante per la valutazione.
Le applicazioni e i file Notebook, i documenti computabili, dinamici e interattivi creati con Mathematica, possono essere distribuiti automaticamente su cloud, desktop, server, mobile, sistemi embedded esiti internet.
Ricerca e Sviluppo con Mathematica
Mathematica integra la più grande collezione al mondo di algoritmi, capacità di calcolo ad alte prestazioni e un potente motore di visualizzazione in un sistema coerente e semplice da usare; ciò rende estremamente intuitivo, veloce ed economico il processo di creazione di modelli di calcolo personalizzati e per questo rappresenta lo strumento ideale per la ricerca di base ed applicata in ogni settore.
Cosa è Mathematica
Mathematica: per la moderna computazione tecnica, non c’è altra scelta.
Grazie al significativo sviluppo e alla visione coerente per più di 30 anni, Mathematica è all’avanguardia in una vasta gamma di applicazioni, unico nel supporto agli odierni ambienti e i flussi di lavoro della computazione tecnica.

Un sistema immenso, completamente integrato
Mathematica ha più di 5000 funzioni interne che coprono tutte le area della computazione tecnica, tutte minuziosamente integrate così che possano lavorare perfettamente insieme, e tutte pienamente incluse nel sistema Mathematica.

Non solo numeri, non solo matematica, ma ogni cosa
Costruito in più di 30 anni di sviluppo, Mathematica eccelle in ogni area della computazione tecnica, incluse: reti neurali, machine learnings processamento delle immagini, geometria, Data Science, visualizzazione e molto altro ancora…
Inimmaginabile potenza degli algoritmi
Mathematica offre algoritmi di potenza inimmaginabile in tutte le aree; molti algoritmi sono stati creati da Wolfram utilizzando metodologie di sviluppo e capacità uniche del Wolfram Language.
Livelli progressivi mai cosi avanzati
Superfunzioni, meta-algoritmi… Mathematica fornisce un ambiente progressivamente di livello più avanzato e il più possibile automatizzato, così che il lavoro possa essere il più efficiente possibile.
Ogni caratteristica è di livello industriale
Mathematica è costruito per fornire funzionalità di livello industriale: con algoritmi robusti ed efficienti in tutte le aree, capacità di gestione di problemi su larga scala, parallelismo e computazione GPU e altro ancora…
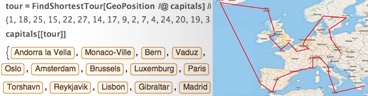
Potente semplicità di utilizzo
Grazie alla potenza degli algoritmi e all’attenta progettazione del Wolfram Language, Mathematica costruisce un sistema dalla semplicità unica, con i suggerimenti predittivi e gli input in linguaggio naturale, e altro…
Sia documenti che codice
Mathematica utilizza l’interfaccia dei Notebook Wolfram per organizzare ogni cosa fatta in un ricco documento che include testo, codice eseguibile, grafici dinamici, interfacce utente e molto altro…
Il codice ha senso
Con il suo sistema coerente che include gli intuiti nomi delle funzioni simili alla lingua inglese, il Wolfram Language, il linguaggio alla base di Mathematica, è univocamente semplice da leggere, scrivere e imparare.
Dai ai tuoi risultati il miglior aspetto
Mathematica presenta i tuoi risultati magnificamente, creando istantaneamente visualizzazioni interattive eccezionali e documenti da pubblicare dall’estetica impeccabile e di qualità professionale.
150.000+ esempi
Inizia qualsiasi progetto con l’aiuto di 150.000+ esempi del Documentation Center, di 10.000 demonstration con il codice aperto nel Wolfram Demonstrations Projects, e centinaia di altre risorse utili.
Dati dal mondo reale continuamente aggiornati
Mathematica ha accesso alle vastissime risorse di conoscenza Wolfram, che includono dati continuamente aggiornati e gratuiti in migliaia di differenti domini.
Integrazione perfetta nel Cloud
Mathematica è ora perfettamente integrato nel Cloud, permettendo la condivisione, la computazione Cloud e molto altro ancora in un unico e potente ambiente ibrido cloud/desktop.

Connesso a ogni elemento
Mathematica è costruito per essere connesso a ogni elemento: più di 180 formati file, altri linguaggi, Wolfram Data Drop, API, database, programmi, dispositivi Internet-of-Things e perfino istanze distribuite di sé stesso.
Approfondimento
Mathematica si basa sul potente Wolfram Language.
» Full Wolfram Language Documentation & Reference
Highlighted Core Areas
Wolfram ha creato una nuova sezione del proprio sito per organizzare e focalizzare l’applicazione di Mathematica e delle Tecnologie Wolfram in alcune Aree scientifiche fondamentali.

Wolfram User Interfaces:
creazione di interfacce utente grafiche e interattive
Automatizza la costruzione dell’interfaccia o crea GUI sofisticate da zero. Distribuisci e condividi facilmente app, notebook, palette e altre interfacce.

Wolfram Machine Learning: Machine Learning e Reti neurali
Altamente automatizzato per i principianti e completamente personalizzabile per gli esperti, oltre a una profonda integrazione con analisi statistiche, visualizzazione, elaborazione delle immagini e altro per creare sistemi intelligenti con qualsiasi tipo di dati.

Wolfram Visualization: visualizzazione scientifica, dati e funzioni
Le visualizzazioni Wolfram semplificano e automatizzano la creazione di grafici utilizzati per comprendere dati e funzioni per ogni cosa, dalle esplorazioni personali ai report e ai documenti pubblicati.

Wolfram Image Computation: elaborazione, analisi e calcolo delle immagini
Per principianti o esperti, Wolfram Image fornisce un set completo ed efficiente di funzioni di elaborazione, riconoscimento e analisi delle immagini, strettamente integrate con funzioni altamente automatizzate di machine learning, statistica, visualizzazione e altro ancora.
Wolfram Calculus & Algebra: calcolo matematico simbolico e numerico
Per tutti, dagli studenti delle scuole medie ai ricercatori matematici avanzati. Secoli di sviluppo nella matematica racchiusi in un insieme di funzioni eccezionalmente potenti e strettamente integrate con la visualizzazione avanzata e dati immediatamente calcolabili.

Wolfram Optimization: modella, risolvi e analizza i progetti
Wolfram fornisce un set completo di strumenti per elaborare il miglior progetto o prendere la decisione migliore in base ai vincoli presenti, completamente integrato con funzioni di machine learning altamente automatizzate, statistiche, dati incorporati immediatamente calcolabili e altro ancora.
Wolfram FEM: metodo agli elementi finiti
Per principianti ed esperti, Wolfram FEM acquisisce il comportamento del tuo progetto fornendo modelli multifisici di equazioni alle derivate parziali, solutori e funzioni di post-elaborazione senza soluzione di continuità, completamente integrati con funzionalità avanzate di visualizzazione e geometria.

Wolfram Geometry: modellazione geometrica e calcolo
Wolfram fornisce un set completo di strumenti e soluzioni integrati per la modellazione, l’analisi, la visualizzazione e la sintesi della geometria; su misura per esigenze di diverso livello, dai principianti agli avanzati.
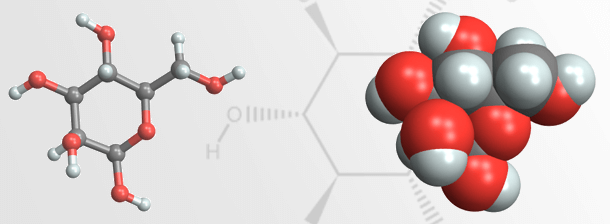
Wolfram Chemistry: modellazione e analisi molecolare e chimica
Per studenti, ingegneri e ricercatori: visualizza, analizza e modella strutture molecolari, reazioni chimiche e altro con funzioni specializzate strettamente integrate con dati proprietari o disponibili pubblicamente.
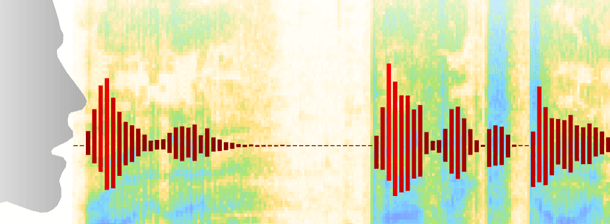
Wolfram Audio Computation: elaborazione e analisi audio
Offre un’elaborazione altamente ottimizzata e un’analisi di alto livello di parlato, musica e altri segnali audio. La stretta integrazione con le funzionalità di Machine Learning e Reti Neurali consente lo sviluppo di soluzioni in sistemi automatizzati, sicurezza, medicina e altro ancora.

Wolfram Video Computation: analisi, montaggio e creazione video
Acquisisci, crea o elabora file video utilizzando funzioni video eccezionalmente potenti e flessibili, basate su capacità ottimizzate di gestione immagini e audio e strettamente integrate con visualizzazione avanzata, machine learning automatizzato e altro ancora.
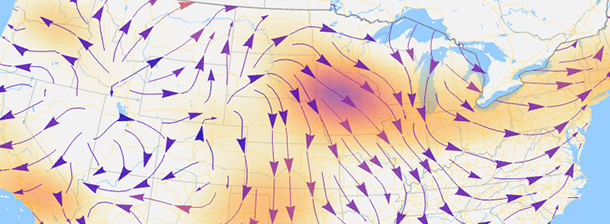
Wolfram Geography: analizzare, calcolare e visualizzare i dati geografici
Rendi la geografia calcolabile con dati geografici curati, calcoli precisi e visualizzazione automatizzata. Per principianti ed esperti, converti facilmente i tuoi dati in mappe dettagliate e di bell’aspetto.
Wolfram Control Systems: modellazione, progettazione, distribuzione
Modella l’ambiente. Progetta un controllore. Distribuisci nel mondo reale. Tutto in un flusso di lavoro altamente integrato, sviluppato per studenti e professionisti.
Wolfram Tools for AIs: superpotenza computazione intelligente per l’Intelligenza Artificiale
Connetti LLM e altri sistemi di intelligenza artificiale a computazione e conoscenze potenti, accurate e attuali, sia attraverso il linguaggio naturale che il linguaggio computazionale di alto livello.
Wolfram Core Technologies

Wolfram Language
L’esclusivo linguaggio simbolico basato sulla conoscenza che è nato da Mathematica e che ora alimenta il sistema Mathematica.

Wolfram Algorithmbase
La più grande rete integrata di algoritmi al mondo, che fornisce ampie e profonde funzionalità integrate per Mathematica.
Wolfram Notebook Interface
L’interfaccia basata su documenti, unica nel suo genere, che consente di combinare codice eseguibile, testo riccamente formattato, grafica dinamica e interfacce interattive in Mathematica.

Natural Language Understanding
Introdotta in Wolfram|Alpha e ora completamente integrata nello stack tecnologico di Wolfram, la NLU è un elemento chiave in un’ampia gamma di prodotti e servizi Wolfram..

Wolfram Cloud
La tecnologia dell’infrastruttura che consente di eseguire Mathematica Cloud con un semplice browser web.
Wolfram Knowledgebase
La base di conoscenze, unica nel suo genere, continuamente aggiornata, che alimenta Wolfram|Alpha e fornisce dati computabili del mondo reale da utilizzare nei prodotti Wolfram.
The Mathematica Trajectory
In tre decenni è stata fatta molta strada
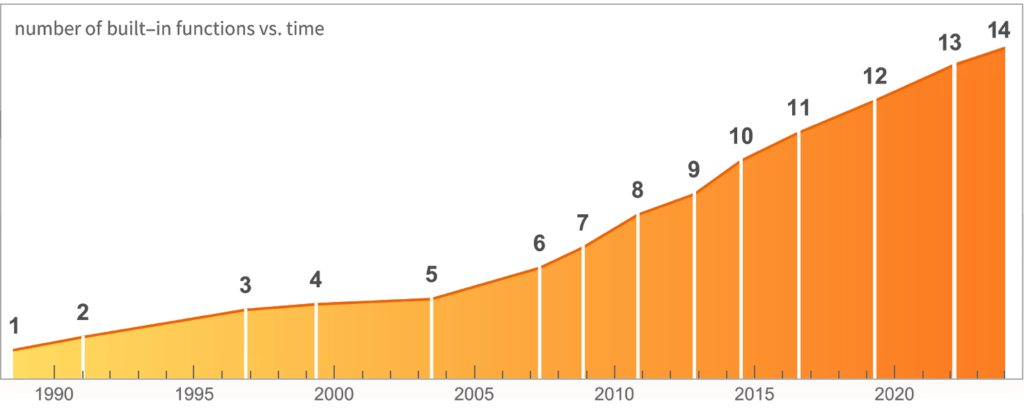
Le oltre 500 funzioni di Mathematica 1 sono ancora presenti in Mathematica 13, ma ora ce ne sono più di 6.000, oltre a una vasta gamma di nuove idee importanti che ampliano notevolmente la visione e la portata del sistema.
The 1988 Revolution
When Mathematica first appeared in 1988, it revolutionized technical computing—and every year since then it’s kept going, introducing new functions, new algorithms and new ideas.
Far, Far Beyond Math
Math was Mathematica’s first great application area—and building on that success, Mathematica has systematically expanded into a vast range of areas, covering all forms of technical computing and beyond.
The Innovation Gets Even Faster
Mathematica has followed a remarkable trajectory of accelerating innovation for three decades—made possible at every stage by systematically building on its increasingly large capabilities so far.
Serious New Ideas in Every Version
Versions of Mathematica aren’t just incremental software updates; each successive one is a serious achievement that extends the paradigm of computation in new directions and introduces important new ideas.
What You Learned in Version 1 Still Works
If you’re one of the lucky people who used Mathematica 1, the code you wrote over three decades ago will still work—and you’ll recognize the core ideas of Mathematica 1 in the vast system that is Mathematica today.
Always Moving Forward, for three decades
Mathematica has always stayed true to its core principles and careful design disciplines, letting it continually move forward and integrate new functionality and methodologies without ever having to backtrack.
Le novità di Mathematica 14.x
Sulla base di oltre un terzo di secolo di costanti innovazioni, Mathematica spinge i confini del calcolo moderno come mai prima d’ora.
Novità introdotte da Mathematica 13 …
Le novità in Mathematica 14.2 | Gennaio 2025
Version 14.2 introduces a powerful tool in Tabular, which provides a very streamlined and efficient way to handle tables of data laid out in rows and columns, with hundreds of other functions enhanced to make use of its special features. Additional new functions and improvements have been added to enhance neural nets and LLMs, work with game theory, improve GPU computation, and expand images and videos.
- Create a version of a function protected against bad input with Failsafe
- Delete elements not obeying a criterion function with Discard
- Use AssociationComap to create an association by applying a list of functions to a value
- Display an expression completely shielded from evaluation with HoldCompleteForm
- Tabular represents column-oriented tabular data with different types, missing values, etc.
- ToTabular converts to Tabular with detailed control
- Multiple new functions introduced to support Tabular operations: FromTabular, TabularQ, TabularColumn, TabularRow, TabularSchema, ColumnKeyExistsQ, TabularQ, TabularColumnQ and TabularRowQ
- Several built-in functions have been updated to support Tabular natively, including Part, Take, Drop, TakeDrop, Key, KeyDrop, KeyTake, Select, Discard, TakeSmallestBy, TakeLargestBy, MaximalBy and MinimalBy
- Many Import formats have been added or updated to support tabular data, such as CSV, XLSX, XLS, ODS, SXC, TSV, Table, Parquet, ArrowIPC, ORC, ArrowDataset, SAV, SAS7BDAT, DTA, POR, XPORT, RData, RDS and DIF
- DataConnectionObject allows for connecting to data stores (with authentication, queries, etc.) such as “AmazonS3”, “AzureBlobStorage”, “Dropbox” and “IPFS”
- DatabaseReference updated to allow relational databases to be used as out-of-core back ends for Tabular
- Return an in-memory version of an out-of-core object with ToMemory
- Handle missing and outlier values in tabular data with TransformMissing and TransformAnomalies, respectively
- Spread values from a single column into several columns with PivotToColumns; inversely, gather values from several columns into one column with PivotFromColumns
- Use TransformColumns to compute columns from values in each row
- Perform simple or grouped aggregation with AggregateRows
- Compute a pivot table with multiple row and column pivots and aggregation with PivotTable
- Many visualization functions have been updated to support plotting values from tabular columns, including BarChart, PieChart, BubbleChart, Histogram, DateHistogram, ListPlot, ListLinePlot, ListPlot3D, StackedListPlot, DateListPlot and more
- Perform asynchronous LLM generation with LLMSynthesizeSubmit and ChatSubmit
- Multiple machine learning and neural network functions have been updated to support Tabular, including Classify, Predict, ClassifierMeasurements, PredictorMeasurements, FindClusters, LearnDistribution, FeatureExtraction, DimensionReduce, FeatureSpacePlot, NetTrain and NetMeasurements
- Represent a simultaneous game specified by payoff matrices or arrays with MatrixGame
- Find Nash equilibria in a MatrixGame with FindMatrixGameStrategies
- Visualize matrix games and strategies with MatrixGamePlot
- Represent a sequential game specified by a game tree with TreeGame
- Find subgame perfect equilibria (SPE) for a TreeGame with FindTreeGameStrategies
- Visualize tree games and strategies with TreeGamePlot
- Simplify or expand symbolic array expressions with ArraySimplify and ArrayExpand, respectively
- Use ComponentExpand to expand a symbolic array expression into its component parts
- Find the instant of relevant astronomical events with FindAstroEvent
- MidDate computes the midpoint date of a granular date or list of dates
- GPUArray stores data in memory accessible for GPU-accelerated computation
- Multiple built-in functions have been updated to support GPUArray, including ArrayDepth, Dimensions, Length, Part, Dot, Transpose, ConjugateTranspose, Diagonal, Tr, LinearSolve, Fourier, SeedRandom, RandomInteger, Mean, Variance, Min, Max, Plus, Times, Total, Sin, Cos, Tan, ArcSin, Exp, Log and more
- Detect and track objects in a video with VideoObjectTracking
- Highlight objects in a video with HighlightVideo
- Use SubtitleStyle to specify style for created subtitle tracks
- MagnetostaticPDEComponent models magnetostatics without currents
- MagneticPDEComponent models quasistatic magnetic fields with currents
In addition to the features introduced in Version 14.2, 908 bugs were fixed in this release cycle.
- AstroGraphics has wrong default AstroRange when plotting data over the whole sky (452857)
- Variance of WeightedData objects returns wrong value (452706)
- STL exporting can create incomplete models (451972, 452302)
- DateListPlot missing X-axis ticks when specifying FrameTicks (450764)
- ListAnimate jumps to the beginning with fps specified and AnimationRepetitions -> 1 (333899)
- An integral involving a positive integrand over a four-dimensional unit cube is giving a negative result on macOS (427726)

Le novità in Mathematica 14.1 | Luglio 2024
Version 14.1 introduces the unified Wolfram application and expands Wolfram Language by offering new tools for working with neural nets and LLMs, for finding differences in content, for working with images and videos, and for exploring scientific evaluations through biomolecules, astrophysics and more.
- Flip one of the bits of an integer number with BitFlip
- Added several functions to test elements of a list: AllSameBy, AllMatch, AnyMatch, NoneMatch
- LLMPromptGenerator allows adding context-dependent messages to an LLM prompt
- Search in a text corpus by semantic similarity with SemanticSearch
- Create and update semantic similarity indices with CreateSemanticSearchIndex and UpdateSemanticSearchIndex
- New service connections to LLMs: AlephAlpha, GoogleGemini, MistralAI, Cohere, DeepSeek, TogetherAI and Groq
- Create, update and search vector databases with CreateVectorDatabase, AddToVectorDatabase and VectorDatabaseSearch
- Support for symbolic vector, matrix and array symbols with VectorSymbol, MatrixSymbol and ArraySymbol
- Added support for symbolic vectors, matrices and array inputs to numerous functions, including D, Grad, Div, Laplacian, Transpose, TensorTranspose, Dot, Cross, TensorContract and more
- Standard constructors needed for symbolic vector, matrix and array formulas added: SymbolicZerosArray, SymbolicOnesArray, SymbolicIdentityArray and SymbolicDeltaProductArray
- Stability analysis for systems of differential equations added with DStabilityConditions
- Stability analysis for systems of difference equations added with RStabilityConditions
- Added versions of the trigonometric functions for use with degree arguments: SinDegrees, CosDegrees, TanDegrees, CotDegrees and more
- PascalBinomial is a binomial that preserves Pascal’s identity for all integers
- Conform a list of dates or times to have shared granularity and calendar with ConformDates
- Descriptive statistics functions like Mean, Median, Variance, Correlation and others have been updated to work on dates and time data
- AstroRiseSet computes rise and set times for any astronomical object, observed anywhere on any date
- PolarCurve represents curves in polar coordinates
- Count triangle cycles in a graph with GraphTriangleCount
- ManipulateVideo creates a video from Manipulate using keyframe parameters
- Sow video snippets to later reap the full video with SowVideo and ReapVideo
- VideoFrameFold transforms a video using a stateful iteration
- Add a subtitle track to video from audio transcription with VideoTranscribe
- Plot a summary of the video and audio tracks with VideoSummaryPlot
- Multiple functions that take audio input, such as AudioAmplify and AudioNormalize, now also work on video input
- ElectricCurrentPDEComponent models electric currents in PDEs
- VonMisesStress computes the von Mises stress from a stress tensor
- View the differences between two notebooks, files, strings, lists, etc. with Diff
- Perform a three-way diff on supported diff targets with Diff3
- Apply a diff change set to an existing object with DiffApply
- FunctionCompile has been updated and now reports progress and gives a detailed report on compilation errors; it also now supports the CompilerRuntimeErrorAction option, which controls behavior when errors are encountered running compiled code
- Symbolic representation of external operations added with ExternalOperation
- $DistributedDefinitions and ClearDistributedDefinitions return and clear the list of all symbols whose definitions have been distributed to parallel subkernels, respectively
In addition to the features introduced in Version 14.1, 1,280 bugs were fixed in this release cycle.
- DateObject does not parse ISO 8601 week dates correctly (446892)
- GeoBounds can give incorrect results when subregions touch (445429)
- ImageToolbar coordinates tool does not return the correct (x, y) coordinate values (410592)
- MeanAround returns inconsistent results with Quantities (409665)

I Princìpi di Mathematica
Oggi esistono molti software specialistici e per ciascun settore scientifico esistono pacchetti estremamente efficienti nella soluzione del singolo problema.
Questa iper-specializzazione però, se da un lato risponde in maniera esatta al singolo quesito, dall’altro porta notevoli difficoltà quando si cerca di usare uno di questi software in ambiti più generali, ovvero in applicazioni che si discostano da quelle per le quali il programma è stati costruito.
In questi casi è necessario rivolgersi a un nuovo software specialistico per la soluzione della nuova problematica. Questo comporta il dover ricominciare la formazione per la comprensione del nuovo programma, dall’interfaccia ai comandi; in senso più ampio è necessario un lungo periodo di avviamento per capire la filosofia del nuovo pacchetto.
Mathematica è un software di più ampie vedute e di infinite applicazioni pratiche, lo dimostra il fatto che è il software di riferimento nelle più disparate aree: dalla chimica all’econometria, dall’ingegneria alla biologia, dall’astrofisica alla teoria della musica.
Mathematica è stato concepito secondo princìpi molto robusti, e questo gli ha permesso di espandersi da un nucleo centrale primario a una moltitudine di applicazioni scientifiche con un approccio univoco basato su una filosofia semplice e immutata nelle versioni: “Tutto è una funzione”.
Un software che è nato basandosi su principi garantisce che, con il passare degli anni, non ci saranno sorprese, perché le aggiunte nelle nuove versioni non saranno parti in disaccordo con il nucleo del programma o modifiche in corso d’opera per aggiustarne falle tecniche, saranno invece la naturale evoluzione.
La filosofia di Mathematica e i suoi principi hanno portato il software molto lontano sbaragliando programmi che erano nati privi di fondamenti e creando i presupposti per far nascere Wolfram|Alpha: il motore di calcolo della conoscenza.
Perché usare Mathematica?
Perché i princìpi contano.
Oltre tre decenni di costruzione su solidi principi di progettazione fanno di Mathematica la piattaforma di calcolo più avanzata al mondo.
Automation
L’automazione è la chiave per un calcolo produttivo. A differenza di altri sistemi, Mathematica applica un’automazione intelligente in ogni parte del sistema, dalla selezione degli algoritmi al layout dei grafici e alla progettazione dell’interfaccia utente. Si ottengono risultati affidabili e di alta qualità senza bisogno di competenze sugli algoritmi e, anche se si è esperti, si ottengono risultati più rapidamente.
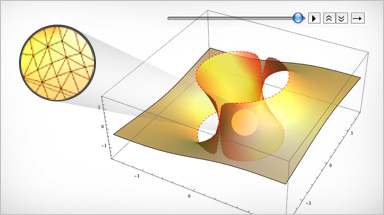
Integrated All-in-One Platform
I software specializzati e i pacchetti di strumenti aggiuntivi scoraggiano l’esplorazione creativa di nuove idee e aree: un costo ancora maggiore del loro prezzo di acquisto. Mathematica non richiede componenti aggiuntivi. È dotato di funzionalità specializzate integrate per molte aree tecniche, dalla biologia computazionale all’analisi wavelet, tutte strettamente integrate con il resto del sistema.

Hybrid Symbolic-Numeric Methodology
Il calcolo simbolico e quello numerico sono tradizionalmente considerati separati, a scapito degli utenti. In Mathematica sono perfettamente integrati, consentendo metodi ibridi unici per molti problemi e garantendo risultati coerenti ogni volta che si combinano quantità di qualsiasi precisione.
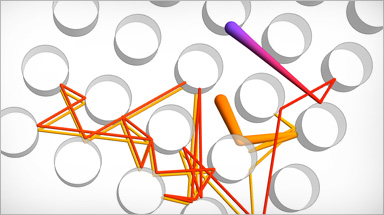
Multiparadigm Language
Nessuno stile di programmazione è ideale per ogni problema. Mathematica si distingue dai linguaggi tradizionali per il fatto di supportare contemporaneamente molti paradigmi di programmazione, come quello procedurale, funzionale, basato su regole, su modelli e altri ancora.
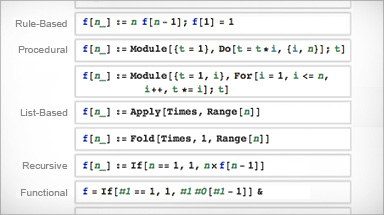
Built-in Knowledge
La ricerca e l’aggiornamento di set di dati standard non devono interrompere il flusso di lavoro. Mathematica è unica tra le piattaforme di calcolo tecnico perché include una vasta collezione di dati curati di ogni tipo, continuamente aggiornati e ampliati.
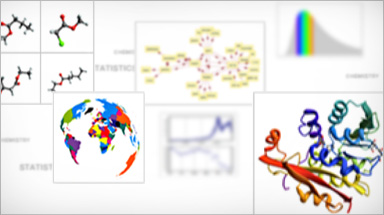
Document-Based Workflow
Non dovrebbe essere necessario un programma per elaborare i dati, un altro per visualizzarli e un terzo per presentarli in modo interattivo. Mathematica fa tutto in un unico flusso di lavoro, tenendo insieme tutti gli elementi di un progetto: calcoli, visualizzazioni, dati, documentazione e persino applicazioni interattive, in documenti unici e flessibili.
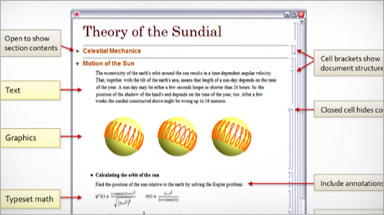
Piattaforme Disponibili per Mathematica
Mathematica viene fornito come licenza singola sempre in versione Desktop e Cloud, mentre come licenza network in versione Desktop ed è possibile aggiungere la versione Cloud come opzione.
Mathematica è 64 bit ed è compatibile con le versioni più recenti dei sistemi operativi Windows, Macintosh, Linux.
Per il dettaglio delle Piattaforme Disponibili e i Requisiti di Sistema per la versione corrente di Mathematica, consultare la pagina del sito Wolfram System Requirements …
Mathematica Cloud
Mathematica Cloud brings the world’s ultimate computation system to the modern cloud environment. Use the power of Mathematica interactive notebooks to work directly in your web browser—with no installation or configuration required—and seamlessly share documents and resources in the cloud.
Condivisione e Collaborazione con i Notebook Wolfram
Breve video di 2 minuti che illustra come i Notebook Wolfram non sono solo un eccezionale ambiente di sviluppo, ma possono facilitare la collaborazione con i colleghi nel cloud.
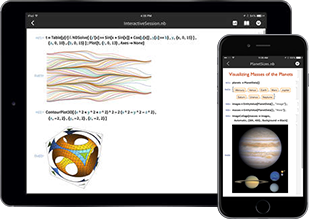
All You Need Is a Web Browser (or a Mobile App)
With Mathematica Cloud, you can go to any web browser and immediately compute with Mathematica or read, author or interact with any Wolfram Notebook.
DESKTOP & MOBILE
Use Mathematica Cloud from any web browser, and view, edit and interact with notebooks on a mobile device with the Wolfram Cloud app.
INTERACTIVITY IN THE CLOUD
Use Manipulate, 3D graphics and other interactive functions directly in your browser.
EMBED WEB CONTENT
Integrate videos and other web content directly into your Mathematica notebooks.
COMPUTE IN THE CLOUD
Perform any Mathematica computation directly in your browser.
ALWAYS THE LATEST VERSION
Mathematica Cloud is automatically updated in the cloud; you don’t have to do anything.
Build your Mathematica notebooks in your browser with rich formatting and structure.
Everything Is in the Cloud
Mathematica Cloud uses the Wolfram Cloud to let you get instant access—and instant sharing—of all your Mathematica material.
INSTANT SHARING
With a few clicks, you can make any Mathematica Clouddocument accessible to anyone you designate.
PERMISSIONS CONTROL
Specify who can read, write, run and interact with any document.
JUST SEND A URL
With Mathematica Cloud, you can refer to any Mathematica notebook just by giving its URL.
AUTOMATIC SAVING
All your Mathematica notebooks are continually saved in the cloud.
Store your data in the cloud and retrieve it from anywhere.
Seamlessly Integrated with the Desktop
Mathematica Cloud is engineered to be completely interoperable with Mathematica on the desktop.
UPLOAD ANY NOTEBOOK
Mathematica Cloud lets you run notebooks created on the desktop.
DOWNLOAD FOR OFFLINE USE
Mathematica Cloud lets you download any cloud notebook for use in Mathematica on the desktop.
ACCESS CLOUD FUNCTIONS FROM THE DESKTOP
Built-in functions let you immediately perform cloud operations from Mathematica on the desktop.
CONTROL THE CLOUD FROM THE DESKTOP
Anything in the cloud can be scripted from Mathematica on the desktop.
Wolfram Cloud Credits
I Crediti Wolfram Cloud sono la valuta di Wolfram Cloud.
Ogni abbonamento a un prodotto Wolfram Cloud include una fornitura di crediti per alimentare le implementazioni e alcune funzioni. Sono inoltre disponibili crediti aggiuntivi che consentono ai progetti di scalare rapidamente.
Cloud Basic plan (free)
La licenza Wolfram Cloud Basic Plan offre un accesso gratuito e introduttivo a Wolfram Cloud per uso non professionale.
Questo tipo di licenza gratuita ha alcune limitazioni tra cui lo spazio di storage limitato e che l’archiviazione dei file e distribuzioni è temporanea (scade dopo 60 giorni).
Per sapere nel dettaglio quali sono tutte le limitazioni del piano Wolfram Cloud Basic Plan vedere la pagina del sito Wolfram…
Aggiungere potenza di calcolo grazie a gridMathematica
Controllate facilmente CPU e GPU per risolvere rapidamente problemi di grandi dimensioni.
Consente di estendere le capacità di parallelizzazione integrate in Mathematica. gridMathematica esegue più task in parallelo, su più CPU e GPU, per un’esecuzione più rapida. Con gridMathematica, il controllo e la gestione dei processi sono completamente automatizzati. I task paralleli appropriati vengono eseguiti più velocemente senza bisogno di modifiche al codice..

Fornendo un pool gestito in rete di almeno 16 kernel di calcolo, gridMathematica può essere condiviso da un gruppo di utenti Mathematica a livello locale e può essere eseguito su hardware remoto per combinare la potenza di più computer.
Il calcolo parallelo è diventato uno standard con Mathematica
Ogni copia di Mathematica include la capacità di calcolo parallelo istantaneo senza alcun costo aggiuntivo. Nelle configurazioni a macchina singola, Mathematica include la capacità di calcolo su quattro, otto o sedici core di processore locale, a seconda dell’edizione di Mathematica in uso. Con l’acquisto di una Mathematica Core Extension, è possibile aumentare il supporto dei core del processore locale di almeno il 50%.
Gli abbonati al Premier Service e gli utenti di gridMathematica ricevono anche l’uso gratuito di Wolfram Lightweight Grid Manager, un programma che semplifica agli utenti la ricerca e l’uso di installazioni di Mathematica su macchine remote e la creazione di griglie ad hoc alimentate da processi del Wolfram Engine non utilizzati.
Cosa è gridMathematica?
gridMathematica è un sistema di estensione integrato per aumentare la potenza delle licenze di Mathematica. gridMathematica Server offre agli utenti di Mathematica un pool condiviso di almeno sedici kernel di calcolo Mathematica aggiuntivi abilitati alla rete per l’esecuzione di calcoli paralleli distribuiti su più CPU.
Non è necessario modificare il codice parallelo esistente: basta rendere disponibile gridMathematica Server e i programmi paralleli possono utilizzare automaticamente la potenza della CPU aggiuntiva. Sia che si tratti di un’attività parallela massiccia, sia che si desideri solo una piccola spinta, è possibile ottenere rapidamente un po’ di potenza in più quando se ne ha bisogno.
LOCAL HARDWARE
Tutti i kernel aggiuntivi vengono eseguiti
su ogni macchina dell’utente.

HIGH-PERFORMANCE CLUSTER
Un cluster dedicato di macchine che eseguono
un sistema di gestione della griglia specializzato.

AD HOC GRID
Un network di diverse macchine disponibili
per il calcolo parallelo.

Per saperne di più sul calcolo ad alte prestazioni con le tecnologie Wolfram:
gridMathematica fornisce:
Distribuzione in rete di tutte le funzionalità di Mathematica, comprese le sue routine numeriche all’avanguardia e superveloci, l’elaborazione delle immagini, le statistiche e le capacità finanziarie. Supporta anche l’accesso remoto alle GPU e la generazione e la compilazione distribuita al volo di codice C parallelo. Se si può fare in Mathematica, si può fare sulla griglia.
Un linguaggio di programmazione parallelo di alto livello, che automatizza gran parte delle comunicazioni, della sincronizzazione, del trasferimento dei dati e del recupero degli errori che di solito rendono il grid computing così difficile da configurare. Grazie al trasferimento automatico dei dati serializzati, è possibile inviare qualsiasi dato e programma strutturato a macchine remote senza dover configurare un file system comune.
Supporto per gli standard HPC, compresi i sistemi di gestione cluster Altair PBS Professional, Microsoft Windows Compute Cluster Server, Microsoft HPC Server, Platform LSF e Sun Grid Engine e include il software Wolfram Lightweight Grid per i sistemi senza gestione cluster. Sono supportate reti Gigabit e ad alta velocità e hardware GPU CUDA e OpenCL.
Per maggiori informazioni consultare le FAQ su gridMathematica